MÉTODO DE TRAPECIO

-

 La regla del trapecio es uno de los métodos más utilizados para calcular aproximaciones numéricas de integrales definidas. Es la primera de las fórmulas cerradas de integración de  Newton – Cotes, para el caso cuando el polinomio interpolante es de grado uno.

Para el polinomio interpolante de primer grado se tiene:

A=∫baf(x)dx≅∫baf1(x)dx, donde
f1(x)=f(a)+f(b)−f(a)b−a(x−a)

Precisamente el área bajo la recta es una aproximación de la integral ∫baf(x)dx, es decir que A=∫ba[f(a)+f(b)−f(a)b−a(x−a)]dx. Luego se tiene que la regla del trapecio viene dada por la fórmula:

A=∫baf(x)dx≈(b−a)[f(a)+f(b)2]

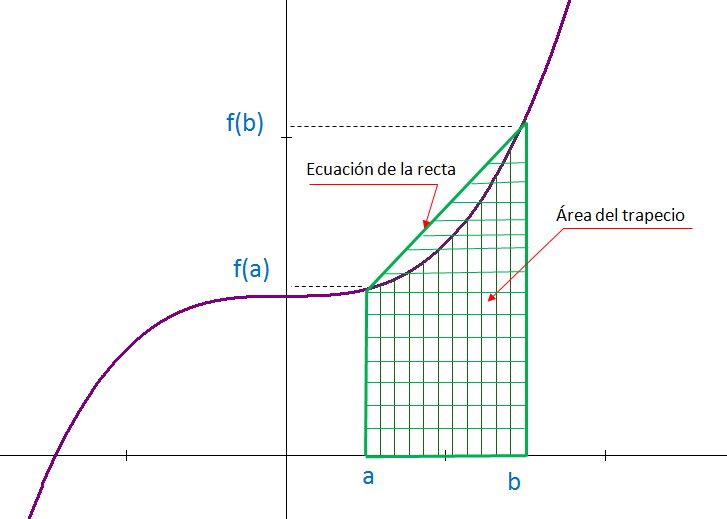
El nombre regla del trapecio se debe a la interpretación geométrica que se hace de la fórmula. Cuando el polinomio interpolante es de grado uno, su gráfica representa una línea recta en el intervalo [a, b] que es el área del trapecio que se forma, como se muestra en la figura.

regla de trapecio

Ejemplo 1

Calcular la integral de f(x)=x3−6x2+11x−6, en el intervalo [1.3, 1.8] aplicando la regla del trapecio.

Solución

  • Con la ayuda de una calculadora, evaluar la función en los extremos del intervalo f(1.3)=0.357, f(1.8)=0.192
  • Calcular b−a=1.8−1.3=0.5
  • Aplicar la fórmula de la regla del trapecio A=∫1.81.3(x3−6x2+11x−6)dx≅0.5[0.357+0.1922]=

Comentarios

Publicar un comentario

Entradas populares de este blog

Introducción al Cálculo Integral

-
Imagen
                                                1. Introducción a la integral de Riemann Después de Cauchy (siglo XIX) y con el trabajo de Riemann, la integración fue considerada como la operación inversa de la derivación; el cálculo integral consistía esencialmente en el cálculo de primitivas.  La definición de la integral de Cauchy seguía la tradicional aproximación del área por rectángulos tal como se ve en la figura. En este sentido no era nada original; la novedad estaba en el hecho de considerar a la integral como un objeto matemático merecedor de estudio por sí mismo, y en el propósito de atribuirle un significado independiente de las técnicas que pudieran utilizarse en los cálculos, y para entender el significado de la integral de estas nuevas funciones más generales, se vio la necesidad de precisar matemáticamente los conceptos de área y de volumen. En este capítulo vamos a considerar la integral desde un punto de vista esencialmente práctico. Nos interesa la integral como her
Leer más

INTEGRALES BINOMIAS

-
Imagen
 Se trata de integrales de la forma: que incluye integrales de raíces cuadradas (p =  1/2 ), de raíces cúbicas (p =  1/3 ), etc.. Nosotros por comodidad al referirnos a ellas, vamos a hablar de dos tipos:   Obsérvese que las integrales de tipo I son las de tipo general pero con  a=b=n= 1.   Toda integral binómica  tipo general  debe ser transformada a  binómica tipo  I para ser integrada.   En concreto, toda integral binómica tipo general se convirte en tipo I con el cambio: b x n  = a t Esto lo vamos a ver con  un ejemplo , tranformemos a tipo I  la integral: para ello hacemos el cambio:   ahora despejamos  x  y hallamos  dx : y sustituimos en la integral: donde hemos extraido un 2 del parentesis (2 + 2t)¹/², la integral es de tipo I.
Leer más